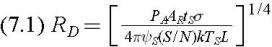Кстати время обзора Ирбиса сектора 100 кв градусов в режиме ВЧП - 2,5-3 сек. (вуду на форумах рассказывает что-то про 10 или 15 секунд . или вллбще 20. короче хрен его знает
Вобуляция частоты повторения зондирующих импульсов в РЛС
В ранее закрытой работе [6] впервые было рассмотрено стохастическое квантование в «медленном времени», как средство устранения эффекта «слепых» скоростей РЛС в режиме СДЦ .
Периодически повторяющиеся «узлы» и «пучности» дисперсии шума квантования вокруг линии «идеального» (многоразрядного) АЦП эквивалентны периодически повторяющимися «слепым» и «оптимальным» скоростям, когда радиальная скорость цели , где , либо , - длина волны, Т- период повторения зондирующих импульсов РЛС.
Фазовое состояние РЛС, задаваемое выбранным значением периода повторения зондирующих импульсов , i = 1, 2, … N, где N – число импульсов в пачке, для каждого определяет регулярное на оси скоростей положение «слепых» и «оптимальных» скоростей и соответствующих им доплеровских частот. Желательно, чтобы соответствовало «оптимальной» скорости, однако при неизвестной скорости цели и в условиях ограничений на диапазон перестройки периода повторения обеспечить это невозможно.
В результате решения вариационной задачи в условиях неизвестной скорости была проведена статистическая оптимизация закона вобуляции частоты повторения (ВЧП) в когерентно-импульсной РЛС с СДЦ.
С математической точки зрения указанная задача по своему содержанию сводилась к решению классической вариационной задачи отыскания минимума определенного интеграла (интеграла Стилтьеса), задаваемого функцией N переменных , удовлетворяющей по каждой переменной граничным условиям и условиям нормировки. Этот интеграл для распределения доплеровских скоростей F(V) являлся функционалом качества:
,
где - N-мерное множество решений, - варьируемые и желаемые скоростные характеристики системы СДЦ и их j -е производные.
Совместная оптимизация алгоритма вобуляции достигалась тем, что значения периодов зондирования выбирались из условия получения требуемой случайной модуляции с учетом корреляционных свойств формируемой последовательности .
Отредактировано dell (2018-07-21 20:39:24)

 Типа вали норы, на западе все сектора работы "стандартные" , русские априори делают гавно, доказательство - слово модератора, который знает матчасть на уровне нуля. Кто не согласен - бан. Хотя там бывают выкладывают в английской части форума интересные картинки.
Типа вали норы, на западе все сектора работы "стандартные" , русские априори делают гавно, доказательство - слово модератора, который знает матчасть на уровне нуля. Кто не согласен - бан. Хотя там бывают выкладывают в английской части форума интересные картинки. 

 "Кто бы это мог быть?"
"Кто бы это мог быть?"